JCO���̓��������
�k�C����w�@�ʎq�G�l���M�[�H�w��U
���q�F�V�X�e���v����H�w����
�� ��i�@ ���� �m��Y
<�@�͂��߂� >
�ȉ��ɐ�������悤�ɁC��������͂ɂ͗l�X�ȃp�����[�^�ɒl��^����K�v������B�����̒l�̕s�m�肳�͉��������̒�ʓI�Ȑ��x�ɉe����^�������łȂ��C����ꍇ�ɂ͎��I�ɈقȂ鋓����^����\��������B����������ŁC�����̒l���m�肷��قǂ̏\���ȏ���肳��Ă��Ȃ��Ƃ����̂�����ł���B
�������C�������ł���܂ł�������ɍ������Ă�����́C����ł������ꂽ����p�������ʂł����J���C��̓��f���̕s��������w�E���Ă��������C�܂��ǂ̂悤�ȏ�K�v�Ȃ̂��𗝉����Ă��������ق����悢�ƍl���C���邱�Ƃɂ����B
< �ڎ��@>
����������͑���i�����E�������l�����Ȃ��ꍇ�̑��j�������j
����������͑���i�������l�������ꍇ�̑��j�������j
��������͑���i�����E�������l�����Ȃ��ꍇ�̑��j�������j
<�@���j����ȈՎZ�o���ɂ��ā@>
�@��������͂ɐ旧���C�ǂ̂悤�ȃp�����[�^�����j�������ɑ傫�ȉe����^����̂��ׂ��B
�@�ՊE���� ��(��)����in - ��w��Tw(��)��0
�@�M���t���� �p(��)�����Aw���Tw�i���j(���M)
��Cf�V���f���(��) (���M)
�@���j������ F ��V���f���(��)�T17
��(Aw�T17/Cf)�(�����in/��w)
�M���t�o�� �p(��)��Aw�(�����in/��w)
�����ŁC�� �F�Ɏ_�E���j���n�t�Ɨ�p���Ԃ̔M�ʉߗ��@
�@�@�@�@Aw �F�`�M�\�ʐ�
�@�@�@�@��Tw(��)�F�Ɏ_�E���j���̉��x�㏸��
�@�@�@�@V �F�Ɏ_�E���j���n�t�̐�
�@�@�@�@��f �F�j�����f�ʐ�
�@�@�@�@T17 �F�ՊE��Ԏ������ԁ@
�@�@�@�@��w �F��p�މ��x�����x�t�B�[�h�o�b�N�W��
�@�@�@�@Cf �F�j����������̕��o�G�l���M�[
�@�@�@�@��in �F��������x
�ȏォ�瑍�j�������́C���C��in�ɔ�Ⴕ�C��w�ɋt��Ⴗ�邱�Ƃ�������Bh�ɂ��Ă͖͋[�������u��p���Ă̔M�`�B�̑���C��in�ɂ��Ă͒��a�����̏Ɏ_�E���j���n�t�ʂ�̌n�̊w�����Ō���ł���ł��낤���C���݂̎��_�ł͂����𐳊m�ɎZ�肷��قǂ̏������ł��Ă��Ȃ��B
<�@���������f���ɂ��ā@>
�@���F�o�� ----�@��_�F�ߎ��C�x�������q�U�Q
�@���n�t���x ----�@�G�l���M�[�ۑ�������
�@�@�@�M�ʉߗ�(h):SUS�e��̔M�`���{�n�t��SUS�e��Ԃ̔M�`�B
�@�@�@�@�@�iSUS�e��Ɨ�p���Ԃ̔M�`�B�͗�p���������z����Ă���
�Ƃ��ĔM�ʉߗ��ɑ傫����^���Ȃ����̂Ƃ��Ė����j
�@�����ː������K�X ---- �o�u�������C�{�C�h�����C�{�C�h���E���f���i�����A�j
�@������M���f���i�����A�j
�@�������x�t�B�[�h�o�b�N�i�����͍l�����Ȃ��j
�@ �@�@�@������in �| ��w��Tw �| ��vVv
<�@�s�m��ȃp�����[�^�ɂ��ā@>
�@���Ɏ_�E���j�����n�t�̕����l�i��M�C��d�C�\�ʒ��́C�S���W���C�M�`�����j
�@�����ː������K�XG�l�@5.0e-7(mol/J)�@�iRPDmail-127�j
�@�������G�l���M�[�������l
�@�@�@�@�@�㏸���F4.2e+7 J/m3�C���~���F0.1�~�㏸���i�����@�C�A�j
�������o�u���̃{�C�h�ւ̍��̎��萔�@2�b�i�����A�j
�@���{�C�h�����x�t�B�[�h�o�b�N�W�� ��v��2.8e-5�i��k/k/cm3�j�i�����@�j
�@��SUS�^���N�Ɨn�t�Ԃ̔M�`�B��
�@�@�@�@�E�����ǖʂɉ������R�Η��Ɋւ���k�b�Z���g���̑��֎��C
�@�@�@�@�E���̔M�����l���g�p�@�@�@�`180W/(m2�K)
���Ɏ_�E���j���n�t�������x
�@��������ꂽ�����x�@�F��in
����ƈ��ɂ��t�@�b�g�}�����ʁ@�F��fat
<�@�g�p�����p�����[�^�@>
�@���������q�����@�@�@�@�@�F3.14e-5�isec�j�@�iRPDmail-176�j
�@�x�������q��s�j�������@�F7.97e-3�@ �@�@�@�iRPDmail-176�j
|
�x�������q�Q |
��i |
��i |
|
1 |
2.70e-4 |
1.26e-2 |
|
2 |
1.73e-3 |
3.17e-2 |
|
3 |
1.56e-3 |
1.15e-1 |
|
4 |
3.14e-3 |
3.11e-1 |
|
5 |
9.28e-4 |
1.40e+0 |
|
6 |
3.38e-4 |
3.87e+0 |
�iRPDmail-176�j
�@SUS�e�풼�a 4.5e-1 (m)
�@SUS�e��� 3.0e-3 (m)
�@SUS�e��M�`���x�@ 14 w/(m�K�j
SUS�^���N�Ɨn�t�Ԃ̔M�`�B�� 180 w/(m2�K�j
�Ɏ_�E���j���n�t�������x�@�@�@25 ��
�Ɏ_�E���j���n�t�̐ρ@�@�@�@�@44 l
�Ɏ_�E���j���n�t��d�@ 1400 kg/m3
�Ɏ_�E���j���n�t��M�@ 4.2 kJ/(kg�K)
�@�@
�{�C�h�����x�t�B�[�h�o�b�N�W�� �@2.8e-5 (��k/k/cm3)
�@��p�މ��x�����x�t�B�[�h�o�b�N�W�� 2.2e-4�i��k/k/K�j�iRPDmail-176�j
�@ �@�@�@ 1.6e-4�i��k/k/K�j�iRPDmail-107�j
�j�����f�ʐρ@�@�@0.063�@(/cm)�iRPDmail-176:��=2.5�Ɖ���j
�����q���ϑ��x�@ 2200 (m)
���z�C�̋C�̒萔�@0.082 �@l�atm/(K�mol)
�j����G�l���M�[������^���@0.93
�j����G�l���M�[�x����^���@0.07
FP���萔�@�@�@�@ �@ 0.004�i/s�j
�@�t�@�b�g�}������(��fat) �@0�@
<�@��͎�@�ɂ��ā@>
�@��_�F�������������Ɋ܂܂��stiffness�ɑΏ����邽��SCM(Stiffness Confinement Method)���̗p�@
|
�@�@�@�@�@�� �� �� �� |
|
|
0 �` 60 �b |
0.0002�b |
|
1 �` 10�� |
0.002�b |
|
10�� �` 17���� |
0.02�b |
<�@��������́F���j�������@>
��in�C��w�Ch���p�����[�^�ɂ��ē�������͂��瑍�j�����������߂��B
�܂��C�ȈՎZ�莮����̊T�Z�l�������B
|
��in ($) |
��w �i����/k�j |
�� |
���j������ |
Q(��) (kw) |
��Tw(��) �i���j |
�ȈՎ� |
|
1.20 |
2.2e-4 |
h |
7.8e+18 |
4.1 |
43.7 |
7.9e+18 |
|
1.05 |
2.2e-4 |
h |
6.9e+18 |
3.6 |
38.3 |
6.7e+18 |
|
1.05 |
1.6e-2 |
h |
9.3e+18 |
4.8 |
51.7 |
9.3e+18 |
|
1.05 |
2.2e-4 |
0.5h |
3.6e+18 |
1.8 |
38.5 |
3.5e+18 |
|
1.05 |
2.2e-4 |
4.0h |
23.5e+18 |
12.9 |
38.5 |
24.8e+18 |
|
0.95 |
2.2e-4 |
h |
6.3e+18 |
3.3 |
34.7 |
6.2e+18 |
|
0.60 |
2.2e-4 |
h |
4.0e+18 |
2.1 |
22.0 |
3.9e+18 |
�ȈՎ��ł���r�I���x�悭���j���������Z��ł���B
<�@��������́F���̑��@>
�@���j�������́C�K�����������ՊE�łȂ��Ƃ��C10��18���ɒB���邱�Ƃ��ł���B
�A0�`60�b�C1�`60���C�P�`17���Ԃ̂����ꂼ��̎��ԑтɂ����ē����I�ȋ����������B
�B0�`60�b�Ԃ̂�����p���[�o�[�X�g���̋����́C��in�CG�l�C�K�X�����G�l���M�[�������l�ɕq���ɉe�������B
�C0�`60�b�̃p���[�o�[�X�g���̋����́C1�`60���C1�`17���Ԃ̋�����j�������ɑ傫�ȉe����^���Ȃ��B
�D1�`60���Ԃ̋����́C��p�މ��x�����x�t�B�[�h�o�b�N�Ə��M�Ɏx�z����C�[���J�̃A���_�[�V���[�g�Ƃ���ɑ����I�[�o�[�V���[�g���ϑ������B�����̃s�[�N�ʒu�͔M�ʉߗ��ɑ傫���ˑ�����B�M�ʉߗ����������قǐU�������������Ȃ�C�U�����傫���Ȃ�B
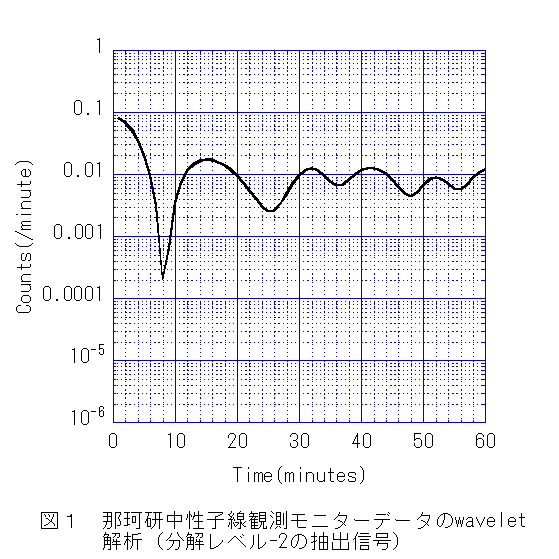
�E�߉ό��̒����q���ϑ����j�^�[�M����wavelet��͂���W�`10���̏��ɃA���_�[�V���[�g�̃s�[�N�ʒu�C16�`18���̏��ɃI�[�o�[�V���[�g�̃s�[�N�ʒu���ϑ������(�}�P�Q��)�B
�F�����q���ϑ����j�^�[��wavelet��͂̃A���_�[�V���[�g/�I�[�o�[�V���[�g�s�[�N�ʒu�Ɠ�������͂ł̃s�[�N�ʒu����v�����邽�߂ɂ́C��L��͂Ŏg�p�����M�ʉߗ����S�{���傫�����Ȃ���Ȃ�Ȃ��B
�@���̒l������͂ɗp����ƁC�ȈՎZ�莮�����������悤�ɁC���j���������S�{���傫���Ȃ�C10��19���ƂȂ�B
�@�̎�n�t��������(RPDmail-152)�ɂ��C���j��������10��18���ł���̂ł��̌��ʂƈ�v�����邽�߂ɂ́C��in�����������邩�C��w��傫������K�v������B
�G��in���������Ȃ�V�i���I�Ƃ��ẮC���̎��̔����x����fat�{��in�ł���C��ƈ��ޔ���Ƀ�in�ƂȂ����Ƃ��l������B
�@�{��͂́C�����͋N����Ȃ����̂Ƃ��ē��������f���ɕ������f����g�ݍ��܂Ȃ������B������L�̉�͏����ł͕����͐����Ă��Ȃ����C���������ɂ���Ă͕������N���肦��i���Ƃ��C��in���傫���C�Ɏ_�E���j���n�t�������x�������Ȃǁj�B���݁C������������悤�ɉ�̓v���O�������蒼���ł���C��L�ɕt���������ʂ�����ꂽ�Ȃ�Ή��߂ĕ���B
<�@�Q�l�����@>
�@�������C���F�g�n�t�R���̌n�̓�������̓R�[�hAGNES�̊J���h�C
JAERI-M(85-212)
�AR.KATO,et.al.(Mistubushi Atomic Power Industries:��CSD):
"The Code Crest to Simulate Criticality Accident Power
Excursion in Fuel Solution", Safety Margin in Critical Safety,
26-30,NOV�DSan Francisco�@U.S.A�D1989
�B�F��������[�����O���X�g�E���[��
RPDmail-107�F�u�ՊE���̉�͕�(���)�vfrom�@�|�c�C�R�{�C���i���j
RPDmail-127�F�uRe.���ː������K�X�v from�@�ΒJ�i����j
RPDmail-152�F�u�j�������v from�@�֖{�i���H��j
RPDmail-176�F�u�v�Z���ʂ̓Z�߁v from�@�ΒJ�C�R���i����j
��������͑���i�������l�������ꍇ�̑��j�������j
< �n�t�t�ʂ���̏������ʂ̕]�� >
�@�O��(RDPmail-191)�ŕ������������f���ɕ�������їn�t�t�ʂ���̏����̃��f����g�ݓ��ꂽ�B
�{��ł́C�n�t�ʂ���̏������ʂׂ��̂ŕ���B
<�@�O��̉�͌��ʂ̊T�v�@>
�@�������l�����Ȃ����f���ł́C���j�������͈�������x�ƏɎ_�E���j���n�t�Ɨ�p���Ԃ̔M�ʉߗ��ɔ�Ⴕ�C��p�މ��x�����x�t�B�[�h�o�b�N�W���ɋt��Ⴗ��B
�A�߉ό��̒����q���ϑ����j�^�[�Ŋϑ����ꂽ�o�[�X�g��̃A���_�[�V���[�g�^�I�[�o�[�V���[�g�ʒu�ƃV�~�����[�V�������ʂ̈ʒu����v�����邽�߂ɂ́C�����ǂɉ������R�Η��Ɋւ��鑊�֎����狁�߂���n�t��SUS�e��Ԃ̔M�`�B�W��h(�`180W/m2�K)���S�{�قǑ傫�����Ȃ���Ȃ�Ȃ��B
�B�S�{�傫���M�`�B�W�����g�p�����ꍇ�C���j�������͂��Ȃ�̉ߑ�]���ƂȂ�B
�C���j�����������������邽�߂ɂ͉��x�t�B�[�h�o�b�N�ȊO�̔����x�⏞���l����K�v������B
�߉ό������q���ϑ����j�^�[�̊ϑ��f�[�^�ɂ́C�o�͂��������Ԃɂ킽���Ēቺ�X���ɂ��邱�Ƃ��ϑ������B�t�ʂ���̏������C���̌��ۂ┽���x�⏞�ƊW�t�����邩����͂����B
<�@�n�t�t�ʍ����Ɣ����x�ω��̊T�Z�@>
�@�����x�⏞�ׂ�ړI�ŁC�����������͉t�ʕ\�ʂ���̏����ɂ�锽���x�ω��ׂ��B(�Q�Q�萔�FRDPmail-176)
|
�n�t������ �i���j |
�n�t���������� (cm) |
�����x�ω��� (��k/k) |
|
0.2 |
0.126 |
-2.97e-3 |
|
0.4 |
0.251 |
-5.96e-3 |
|
0.6 |
0.377 |
-8.98e-3 |
|
0.8 |
0.503 |
-1.20e-2 |
�@�n�t�ʂ̔��ʂ̕ω��������x�ɑ傫�ȉe����^���邱�Ƃ�������B
<�@���j�������̊T�Z�� >
�@���ÓI�ՊE�����@�@��in�|��w��Tw(t)�|��b(t)��0
�@���ÓI�M���t�����@Q(t) = h�Aw���Tw(t)�@�i���M�j
�@�@�@�@�@�@�@�@�@�@�@�@ = Cf�V���f��(t)�@(���M�j
�@�ȏ�̊W������j�������͈ȉ��悤�ɗ^������B
�@�j�������@�@�@�@�@F(t) = V���f���(t)
�@�@�@�@�@�@�@�@�@�@�@�@ = (h�Aw/(Cf���w))(��in�|��b(t)�j
�@�����ŁCh�@�@ �F�Ɏ_�E���j���n�t�Ɨ�p���Ԃ̔M�ʉߗ��@
�@�@�@�@�@Aw �@ �F�`�M�\�ʐ�
�@�@�@�@�@��Tw�@�F�Ɏ_�E���j���̉��x�㏸��
�@�@�@�@�@V�@ �@�F�Ɏ_�E���j���n�t�̐�
�@�@�@�@�@��f �@�F�j�����f�ʐ�
�@�@�@�@�@T17 �@�F�ՊE��Ԏ������ԁ@
�@�@�@�@�@��w �@�F��p�މ��x�����x�t�B�[�h�o�b�N�W��
�@�@�@�@�@Cf�@�@�F�j����������̕��o�G�l���M�[
�@�@�@�@�@��in�@�F��������x
�@ ��b :�����╦���ɂ���ĉt�ʂ��ቺ���邱�Ƃ�
�@�@�@�@�@�@�@ �@����Đ����锽���x�ω�
�@�ȏ�̊W���瑍�j�������͈ȉ��̂悤�ɗ^������B
�@���j����@�@�@�@�@F�� = INTG(T17,0)*F(t)
�@�@�@�@�@�@�@�@�@= Cv�F��
�@�����Ł@�@�@�@�@�@F�� = (Aw�T17/Cf)(h���in/��w)
�@�@�@�@�@�@�@�@�@�@Cv = (1 �| INTG(T17,0)*��b(t)/(��in�T17))
�@(INTG(T2,T1)*f(t)�͊�f(t)��T1����T2�܂Őϕ����邱�Ƃ�\���j
�@������F���͑O��Ŏ������悤�ɕ�����������Ȃ��ꍇ�̑��j�������ł���CCv�͏����╦���ɂ����\�����ƂȂ�B
<�@�n�t�����Ɣ����x�ϕω��@>
�@�n�t����H��Keff�̊W�͈ȉ��̂悤�ɗ^������B
�@keff(H) = �˃�f1/(D1�B2+��r1)
�@ + ��12��˃�f2/((D1�B2+��r1)�(D2�B2+��r2))
�@
�@�@�����Ł@�@B2=(2.405/R)2 + (��/H)2
�@�@�@D1�@�@�F1�Q�g�U�萔�@
�@�@�@D2�@�@�F2�Q�g�U�萔�@
�@�@�@�˃�f1 :���1�Q�j�����f�ʐ�
�@�@�@�˃�f2 :���2�Q�j�����f�ʐ�
�@�@�@��r1 �@:1�Q�����f�ʐ�
�@�@�@��r2 �@:2�Q�����f�ʐ�
�@�@�@��12 �@:1-2�Q�ړ��f�ʐ�
�@�@�@R�@�@ �F�e�풼�a
�@�@�@H�@ �@�F�n�t����
�@���������āCH�̕ω��ɑ��锽���x�ω��͈ȉ��ŗ^������B
�@�@��b(H) = keff(H) �| keff�iHo�j
�@�����ŁCHo�͗ՊE���̗n�t����
< �t�ʂ���̏����Ɖt�ʍ����̕ω� >
�������́C�n�t���x�� SUS�e���C�̈���̏��C�Z�x�ȂǂɈˑ����ĕω����邪�C�����ł͏�����������x�i�ނƁC��C�̈���̏��C���x���O�a��ԋ߂��Ȃ邩�C�n�t���x��
�@�ቺ�̂��߁C�����͋N����Ȃ��Ȃ���̂ƃ��f��������B
�@������Mv(g/cm2�s)�͈ȉ��̂悤�ɕω�������̂Ƃ���B
�@�@dMv/dt = -��Mv
�@�����Ńɂ͏������O�a���萔�B
�@���������Ď���t�ɂ�����������͈ȉ��̂悤�ɗ^������B
�@�@Mv(t)= Mv(0)e(-��t)
�@
�@�n�t�\�ʐς�A�Ƃ������C�����ɂ��n�t������Md(t)�͈ȉ��̂悤�ɗ^������B
�@�@Md(t) = A�INTG(t,0)*Mv(t)
�@ = A�(Mv(0)/��)[1-e(-��t)]
�@�����ɂ��n�t�����̌�����
�@�@��H(t)�@=�@Md(t)/�iA����j
�@�@�@�@�@�@=�@��H��[1-e(-��t)]
�@������ ��H�� = Mv(0)/(�����)�C���͗n�t���x
�@�n�t�����ω��ɔ��������x�ω��͈ȉ��̂悤�ɋ��߂���B
�@�@��b(t) = keff(H) �| keff(Ho�j
�@�@�@�@ �@=�idkeff/dH)��H(t)
�@�@�@�@ �@=�idkeff/dH)��H��[1-e(-��t)]
�@�����ŁCdkeff/dH�� keff �� H �ɑ�����W��
<�@��W���̎Z�o�@>
�@�ȏ�̌v�Z����C��W���͈ȉ��̂悤�ɋ��܂�B
�@�@�@Cv���P-((dkeff/dH)���H��/��in)(1-1/(���T17))
�@��W������C(dkeff/dH)���H������in�ɋ߂��قǁC�܂������傫���قǕ�W�����������Ȃ�C���j���������������Ȃ邱�Ƃ�������B
<�@���������f���̕ύX�@>
�@�O��ł́C�n�t�� SUS�e��Ԃ̔M�`�B�W�������Ƃ��Čv�Z���Ă������C�{��ł͗n�t���x�̕ω��f�ł���悤�ɂ����B�O��ł͓߉ό������q���ϑ����j�^�[�̑O�L�s�[�N�@�ʒu�ƈ�v�����邽�߂ɂ́C���֎����狁�߂��M�`�B�W����4�{�̔M�`�B�W�����K�v�ł��������C�{��̕ύX�ł�3.5�{�ƂȂ�B
<�@��͏����@>
�@�ȉ��Ɏ����p�����[�^�ȊO�̃p�����[�^�̒l�͑O��(RPDmail-190)�̒l���g�p�����B
�@��͏���
�@�@��in�@= 1.05 ($)
�@�@��w �@= 2.2e-4 (��k/k/K)
h* = 3.5h
�t�ʂ���̏��������� : Mv(0) = 5.0e-5 (g/cm2�s)
�������O�a���萔 : ���@�@= 1.6e-4 (/sec)
�@ �@(�߉ό������q���ϑ����j�^�[�E�f�[�^����T�Z)
<�@��������͌��ʁ@>
|
|
�������l�������ꍇ |
�������l�����Ȃ��ꍇ |
|
���j������ |
3.44e+18 |
2.41e+19 |
|
Q(T17) �@(kw) |
0.59 |
13.2 |
|
��Tw(T17)�i���j�@ |
2.7 |
38.4 |
�Z Mv(0)�̒l�͑��j�������ɕq���ɉe����^����B�傫��Mv(0)��^�����17���ԑO�ɗՊE��Ԃ��I������B
�Z ��L��͗�ł́C�ՊE��30���ȓ��ɑ��j�����27%���N����B
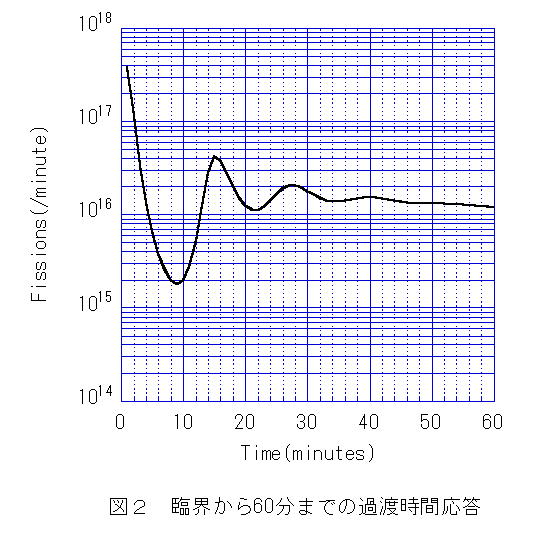
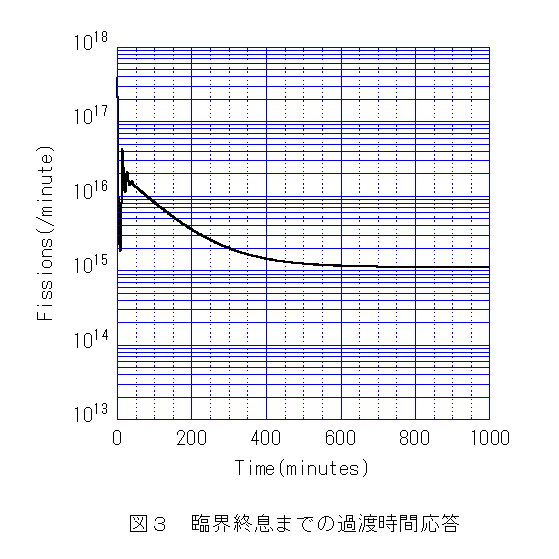
�@�Z �����Ԃɂ킽��o�͒ቺ�X�����t�ʂ���̏����ɂ���čČ��ł���i�}�Q�C�}�R�Q�Ɓj�B
<�@�Q�l�����@>
�B�F��������[�����O���X�g�E���[��
RPDmail-176�F�u�v�Z���ʂ̓Z�߁v from�@�ΒJ�C�R���i����j
RPDmail-191�F�u��������́v �@�@ from�@�ҁC���Ái�k��j